What is a pulley?

A pulley system uses an inextensible string. When one end of the string is pulled by 1 meter, the other end moves by the same distance. This demonstrates the concept of constrained motion or constrained length. Applying a force to one end of the string directly affects the motion at the other end.

We assume that pulleys are massless and frictionless. This implies that when the string is pulled with a force T, the tension in the string is also T. The tension in the other segment of the string is also T, and the pulley is fixed in place. The pulley mechanism does not require additional force to overcome friction. Since the pulley is assumed to be massless, its rotation does not add any load. The friction between the string and the surface of the pulley is infinite. This ensures that the string does not slip along the pulley’s wheel.

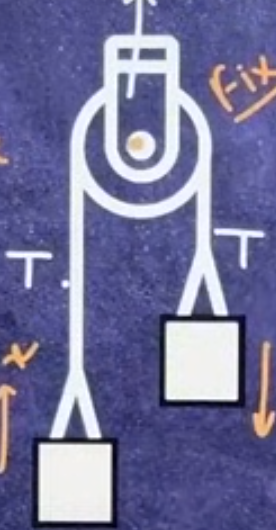
Direction of Tension in the rope of a single fixed pulley. Source- Theory of Physics

Are pulleys always fixed?

Movable pulleys are also used to handle loads when required, and their mechanics differ from fixed pulleys.

In a movable pulley system, when the pulley moves up, for example, it creates a demand for a total rope length of 2x, with x on each side. This additional length must be supplied by the rope. The rope can fulfill this demand either by one end moving up by 2x or by both ends moving up by x each.

This difference is crucial in movable pulley systems because, unlike fixed pulleys, the rope displacement is not necessarily equal to the displacement of the movable pulley. 

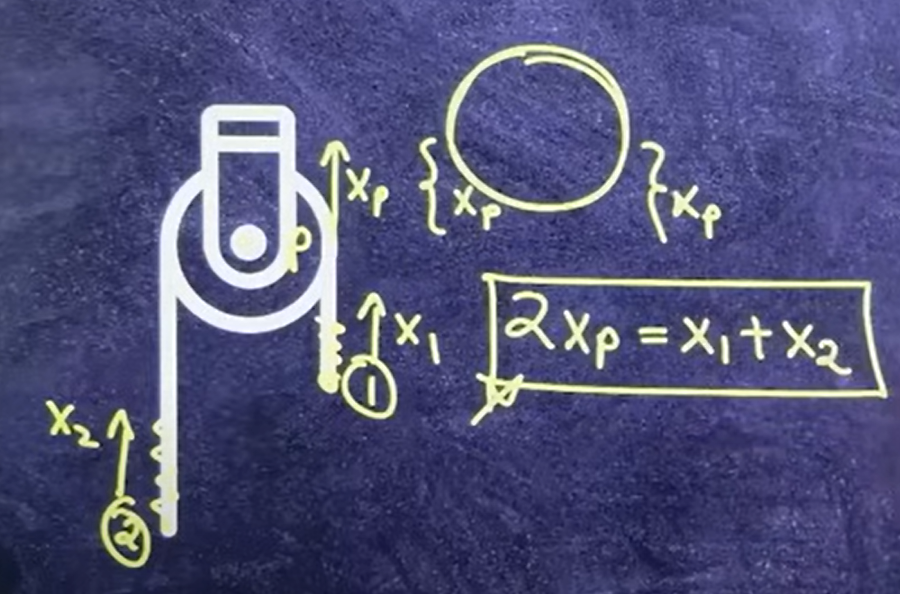
Distance moved by the rope in a movable pulley. Source- Theory of Physics

Combination of pulleys to construct a pulley system

Let us explore how a combination of pulleys functions to understand its applications.

Here, the body attached exerts a tension T on the string, and the tension in the rope on the left is also T. The left side of both strings are fixed. Let the smaller pulley exert a reaction T1 at the string marked with a red dot.

Since the pulley is massless, the force (product of mass and acceleration) is zero. With the resultant force being zero, the downward tension forces (2T) and the upward tension (T1) must balance each other (as shown in the red coloured free body diagram). Therefore, T1 = 2T.

This concept is essential when using combinations of pulley systems.

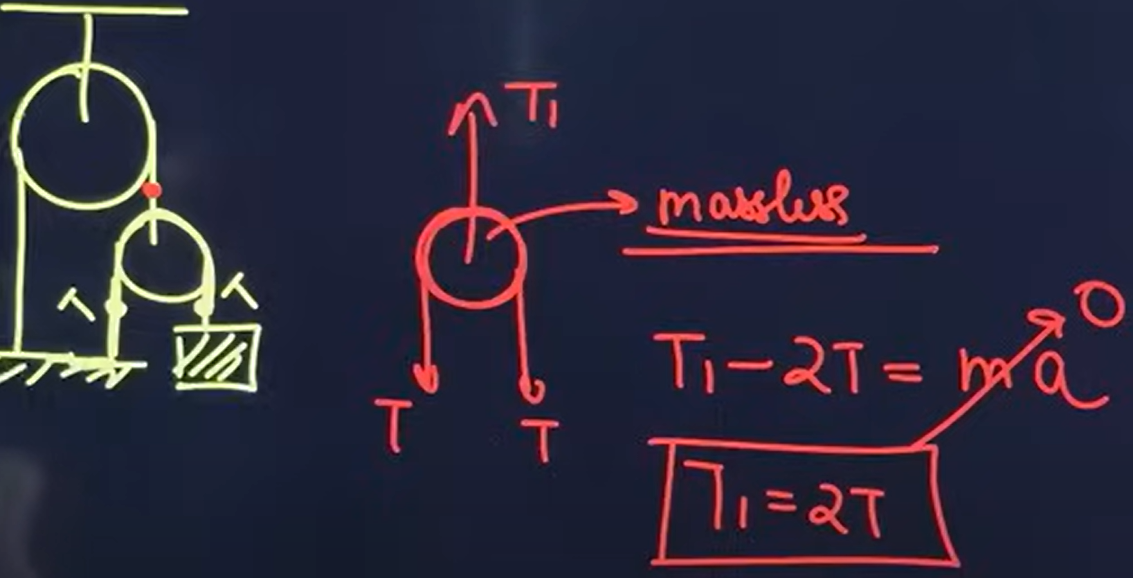
Tension in a movable pulley system. Source- Theory of Physics

Pulley system demonstration model

Labkafe has designed this system of pulleys. This lets you experiment with the weights and tensions needed to balance the pulley system. We will apply the learnings from previous sections to this calculation and understand how much weight can balance the system of pulleys so that they remain at rest. 

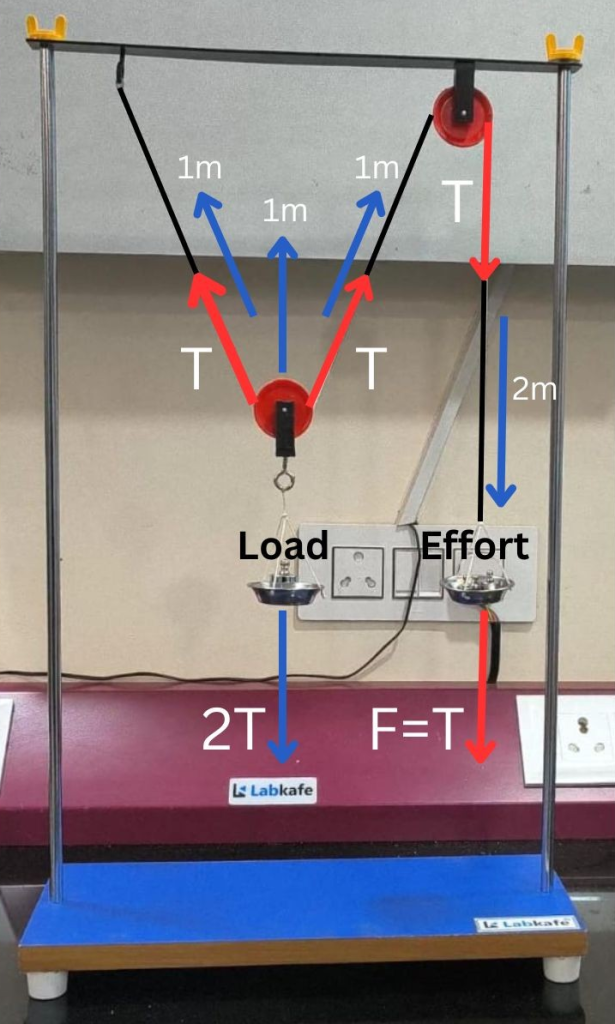
Pulley system demonstration model by Labkafe

Force needed to lift the load using the pulley system

Refer to the image above. Note that the movable pulley at the center supports a load of 2T. This load is carried by two strings attached to the movable pulley. Therefore, the load of 2T is evenly distributed, with each string bearing a tension of T. These tensions are marked in red as T on the two supporting strings.

Now, consider the fixed pulley on the right, which supports a load of T. Since the pulley is fixed, you must apply a minimum force of T to the string on the right side of the fixed pulley. This maintains equilibrium and keeps all the pulleys at rest. These tensions are also marked in red as T on the fixed pulley.

Hence, to lift the load, a minimum force T or F=T must be exerted on the right side string of the fixed pulley. Thus, the net force needed is halved, from 2T to T. This is called mechanical advantage (MA). It is the force amplification factor, represented by the formula Load/Effort. If Load is higher than Effort, then the MA is a natural number. In this case, Load/Effort= 2T/T=2. 

Work done when using the pulley system

It is obvious that using the pulley halves the force or effort needed to lift the load. But what is the work done when you use a pulley, as opposed to lifting the load directly?

In the above image, note that to lift the load by 1m, both the supporting strings on the movable pulley need to move up by 1m each. For this to happen, in the connected pulley system, the fixed pulley string on the right needs to be pulled down by 2m. Hence, the distance moved is doubled, when using this pulley system. 

Work done is force multiplied by displacement or W=F x d.

When you use the pulley instead of lifting the load directly, you halve the force but double the distance. Therefore, the work done effectively remains the same.

This model helps students understand and visualize how pulleys work. While pulley systems might be difficult to relate to by just looking at pictures in the textbook or internet videos, doing the experiment by hand lends crucial tactile engagement. 

To get your own Labkafe pulley system, contact our lab experts today!