Aim:

Using a simple pendulum, plot its L-T2 graph and use it to find the effective length of second's pendulum.

Apparatus:

1. A Clamp With Stand
2. Bob with Hook
3. Split Cork
4. Stop Clock/Stop Watch
5. Vernier Callipers
6. Cotton Thread
7. Half Meter Scale

Theory:

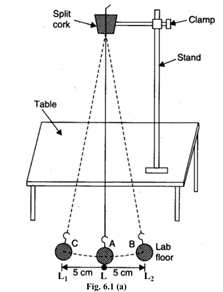
A simple pendulum consists of a heavy metallic (brass) sphere with a hook (bob) suspended from a rigid stand, with clamp by a weightless inextensible and perfectly flexible thread through a slit cork, capable of oscillating in a single plane, without any friction, with a small amplitude (less than 150) as shown in figure 6.1 (a). There is no ideal simple pendulum. In practice, we make a simple pendulum by tying a metallic spherical bob to a fine cotton stitching thread.

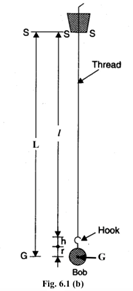
               The spherical bob may be regarded by as a point mass at its centre G. The distance between the point of suspension S and the centre G of the spherical bob is to be regarded as the effective  length of the pendulum as shown in figure 6.1 (b). The effective length of a simple pendulum, L = l + h + r. Where l is the length of the thread, h is length of hook, r is radius of bob.

The simple pendulum produces Simple Harmonic Motion (SHM) as the acceleration of the pendulum bob is directly proportional to its displacement from the mean position and is always directed towards it. The time period (T) of a simple pendulum for oscillations of small amplitude, is given by the relation,

T = 2 π √ (L/g)

Where, g = value of acceleration due to gravity and L is the effective length of the pendulum.

 T2 = (4π2/g) X L             or           T2 = KL (K= constant)

               and,  g = 4π2(L/T2)

If T is plotted along the Y-axis and L along the X-axis, we should get a parabola. If T2 is plotted along the Y- axis and L along the X-axis, we should get a straight line passing through the origin.

Procedure:

1. Find the vernier constant and zero error of the vernier callipers same as experiment 1.
2. Measure the radius (r) of the bob using a vernier callipers same as experiment 1.
3. Measure the length of hook (h) and note it on the table 6.1.
4. Since h and r is already known, adjust the length of the thread l to make L = l + h + r an integer (say L = 80cm) and mark it as M1 with ink. Making L an integer will make the drawing easier. (You can measure the distance between the point of suspension (ink mark) and the point of contact between the hook and the bob directly. Hence you get l + h directly).
5. Similarly mark M2, M3, M4 , M5, and  M6 on the thread as distance (L) of 90 cm, 100 cm, 110cm, 120cm and 130 cm respectively.
6. Pass the thread through the two half-pieces of a split cork coming out just from the ink mark (M1).
7. Tight the split cork between the clamp such that the line of separation of the two pieces of the split cork is at right angles to the line along which the pendulum oscillates.
8. Fix the clamp in the stand and place it on the table such that the bob is hanging at-least 2 cm above the base of the stand.
9. Mark a point A  on the table (use a chalk) just below the position of bob at rest and draw a straight line BC of 10 cm having a point A at its centre. Over this line bob will oscillate.
10. Find the least count and the zero error of the stop clock/watch. Bring its hands at zero position
11. Move the bob by hand to over position B on the right of A and leave. See that the bob returns over line BC. Make sure that bob is not spinning.
12. Now counting oscillations, from the instant bob passes through its mean position L, where its velocity is maximum. So starting from L it traverses LL2, L2L, LL1, L1L hence, one oscillation is completed. We have to find time for 20 such oscillations.
13. Now start the stop watch at the instant the bob passes through the mean position A. Go on counting the number of oscillations it completes. As soon as it completes 20 oscillations, stop the watch. Note the time t for 20 oscillations in the table 6.1.
14. Repeat the measurement at least 3 times for the same length.
15. Now increase the length of the thread by 10 cm or 15 cm (M2) and measure the time t for this length as explained from step 6 to 14.
16. Repeat step 15 for at least 4 more different lengths.

Observations:

Vernier constant

Vernier constant of the vernier callipers, V.C. = ______________ cm

Zero error, ±e = _____________cm

Diameter of the bob and length of hook

Observe diameter of the bob:= (i) ______cm, (ii)________cm, (iii)___________cm

Mean diameter of bob, d0 = _________cm

Mean corrected diameter of bob, d = d0 ±e = __________cm

Radius of the bob, r = d/2= ____________ cm

Length of the hook, h= __________cm

Standard value acceleration due to gravity, g1 : 980 cm s-2

Least count of stop clock = ____________s

Zero error of stop clock = ___________s

Table 6.1 Determination of time-periods for different lengths of the pendulum.

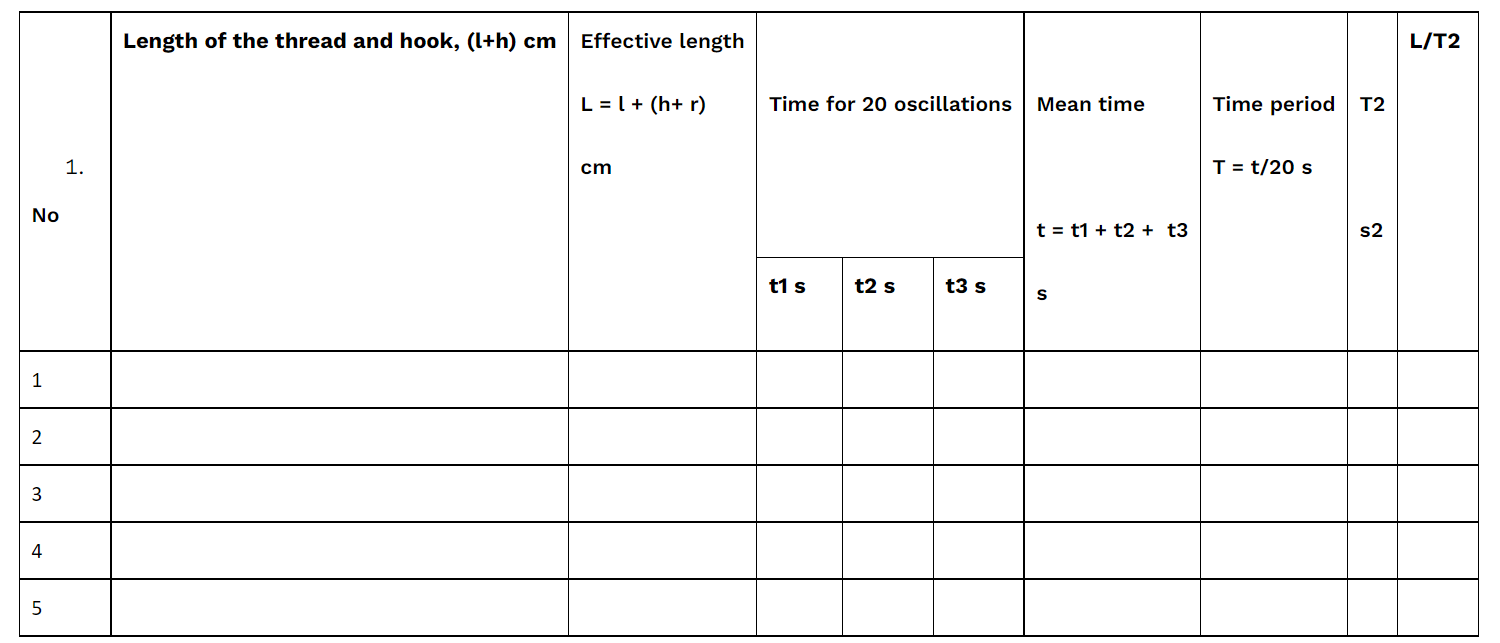
Mean  = L/T2 = _______________________

Calculation:

We know, T = 2 π √ (L/g)

 Experimental value, g1 = 4π2(L/T2) = ______________________

So, %error = (g-g1)/g *100 = ______________________

Graph:

L vs T graph

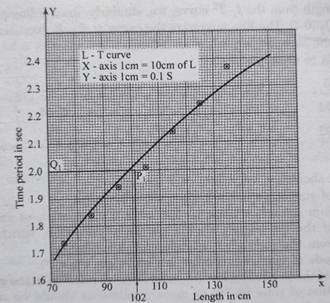
Plot the graph between L and T from the observations recorded in the table 6.1. Take L along X-axis and T along Y-axis. The L-T curve is a parabola. As shown in the figure 6.2. The origin need not be (0,0) point.

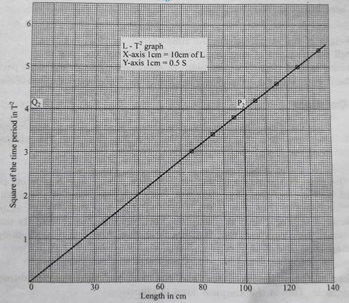
L vs T2 Graph

Plot the graph between L and T2 from the observations recorded in the table 6.1. Take L along X-axis and T2 along Y-axis. The L-T curve is a straight line passing through the (0, 0) point. So the origin of the graph should be chosen (0, 0). As shown in the figure 6.3.

Determination of length of a seconds pendulum from graph:

A second pendulum has time-period 2 s. To find the corresponding length of the pendulum from the L-T graph, draw a line parallel to the L-axis from the point Q1 (0, 2). The line interval the curve L-T at P1. So, the coordinates of P1 is (102, 2).

 Length of the seconds pendulum is _____________(102) cm.

To find the length from the L-T2 curve, we, similarly, draw a line parallel to L-axis is form a point Q2 (0, 4). The line intersects the curve at P2. P2 has coordinates (100, 4).

 Length of the seconds pendulum is _______________(100) cm.

Precautions :

1. The thread should be very light and strong.
2. The point of suspension should be reasonably rigid.
3. The pendulum should oscillate in the vertical plane without any spin motion.
4. The floor of the laboratory should not have vibration, which may cause a deviation from the regular oscillation of the pendulum.
5. The amplitude of vibration should be small (less than 15) .
6. The length of the pendulum should be as large as possible in the given situation.’
7. Determination of time for 20 or more oscillations should be carefully taken and repeated for at least three times.
8. There must not be strong wind blowing during the experiment.

Reference:

1. http://www.ncert.nic.in/
2. https://www.learncbse.in/

you may download Simple Pendulum Experiment Class 11 practical manual .pdf Download Now

About Labkafe: Lab Equipment Manufacturer & Exporter

We are a School laboratory furniture and Lab equipment manufacturer and supplier. In laboratory furniture for school, we first design the entire laboratory room keeping in mind the requirements as per affiliation CBSE Bye-Laws. Also, we take care of the complete designing and installation of laboratory furniture.

In the lab equipment section, we have a wide range of glassware, chemicals, equipment and other lab accessories. Most of them are available for order online on our website but some of them can be procured on demand.

If you have need:-

• laboratory equipment or lab furniture requirements for school
• composite lab equipment list for school
• Physics lab equipment list for school
• Chemistry lab equipment list for
• Biology lab equipment list for school
• Pharmacy lab equipment

do drop a message through chat or mail us at [email protected] or call +919007218364 and we’ll get in touch with you.